头发着色原理
Kajiya-kay着色模型
原理介绍
在前言部分,我们简单了解过这是一种很早提出的头发着色模型,主要是基于Phong式模型进行的改进,因此它是一种不遵守能量守恒的经验模型,但是他可以在使用很小的开销情况下生成一个不错的头发效果,非常适合在实时渲染中使用,因此我们有必要学习一下这个模型。
首先,这个模型将头发纤维抽象化成一个不透明的圆柱体,这个圆柱体既不能透射也不能产生内部反射,因此他不能表现出一些我们观察到的头发的真实效果,尤其是在背光下或者浅色头发的光纤透射效果。它主要是使用Lambert和Phong完成散射和镜面反射的,但是具体的实现又有所不同。
Color=Diffuse(Lambert)+Specular(Phong)
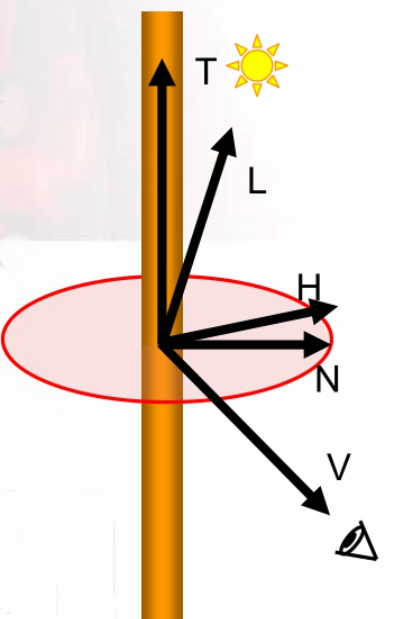
如下图所示,使用一个黄色的圆柱体代表一根头发,T是沿着头发纤维的切线方向,而V是视线,H是L和V生成的半程向量。

Diffuse推导
首先我们给出Diffuse的计算公式:
Diffuse=Kd∗sin(T,L)
我们会发现这与Lambert形式并不是完全一致,这是因为这里我们把头发丝看成一种直径非常小长度还非常长的细丝柱体,因此当我们选取一个光线与头发丝的交点时并不是这个头发丝某一个截面上的某一点,而是看成这个光线与这个截面上的所有点相交,即这个点包含了这个截面上一圈的点,所以他有无数个方向不同的发现,由于是漫散射,所以他是均匀的向四周发散反射光,那么此时我们要计算这个截面上所有的点生成的反射光到视点的能量就变得很复杂,联系BRDF很明显他应该是这个截面上所有点BRDF与入射光的乘积然后在一个半圆形上进行积分,但是由于不同点法线不同那么与光线的夹角也不同,显然此时如果计算cos<N,L>会很困难,因此这样需要计算无数次,那么我们可以换一个角度,由于角<T,L>与<N,L>互余,所以实际上我们可以将入射光与该截面上的各个点的夹角cos值转换为入射光方向L与沿头发丝切线方向T的sin值,这样我们只需要计算次然后再积分即可了,减小了散射计算开销。
Specular推导
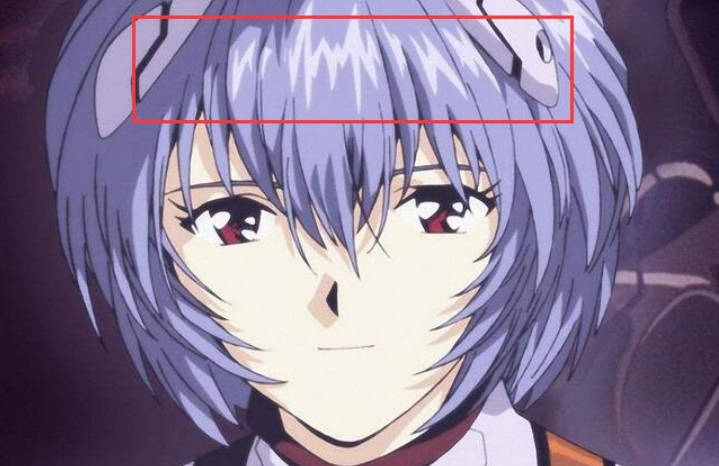
同时对于镜面反射,由于他只向某一个方向反射,这样如果一个个头发丝的计算,那么计算量过大而且计算形式都是重复的,这里我们可以发现实际上头发有一个“天使环”特征如下图所示,即大致上各个头发丝的镜面反射高光位置差不多然后就会形成一个环状高光带

因此我们可以简化一下问题,只需要计算一个头发丝的镜面反射高光,然后再将其纵向环绕一圈自然就绘制出了圆环。我们同样首先给出Specular的公式:
Specular=Ks∗sin(T,H)specularity
我们发现他也与phong不太一样,这是因为上面我提到我们将入射光大到的截面上所有的点看成一个点,而这个点会有无数个不同发现的发现,而如果要用phong计算cos<N,R>(R为反射光,因为先从Phong开始推导)会很困难,先不谈法线选择哪一个,反射光就很难算,因此我们参考bliion-phong知道实际上可以用cos<H,N>来近似代替cos<N,R>因此引入了半程向量,但是法线问题还没有解决,我们同样发现可以使用sin<T,H>来等价表示cos<H,N>因此我们即得到了上面的镜面反射公式。

其实我们如果真的对一个个截面上的点计算镜面反射,会发现反射的光线都是处于同一个圆锥上,这也是我们能够求得一个以后环绕的原因。
缺陷
虽然Kajiya-Kay公式很简洁,但是他却不是基于物理的,这也就导致了头发建模成了不透明的圆柱体,并么有考虑到头发的透光性以及光线在头发中多次折射反射传播的情况,因此不能模拟出背光以及二次高光,因此我们接下来就会介绍一种更加先进的基于物理真实的头发着色模型——Marschner模型。
Marschner着色模型
头发结构
这种模型会将头发视为一种十分透明的椭圆柱体(更加真实),并且实际上他是考虑到了头发的结构分层,同时还考虑到了头发纤维是一种凹凸型表面会对光线产生反射偏移等问题。首先我们看一下头发的结构,我们大致可以将头发分成两层结构:
- 表皮层:这个对于光的散射非常重要,他介于纤维与空气之间,是一种透明介质,同时还会有重叠的嵌套堆叠从而形成凹凸不平的表面,也就会对光线的反射造成偏移,这个我们后面可以使用扰动贴图进行模拟。
- 皮质层:这个是头发纤维的主题,中心就是具有色素的核心髓质,而色素也是确定头发颜色的重要因素。
散射光线的分类
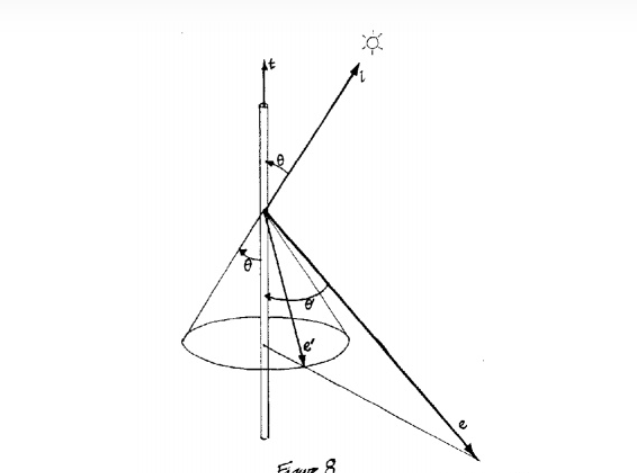
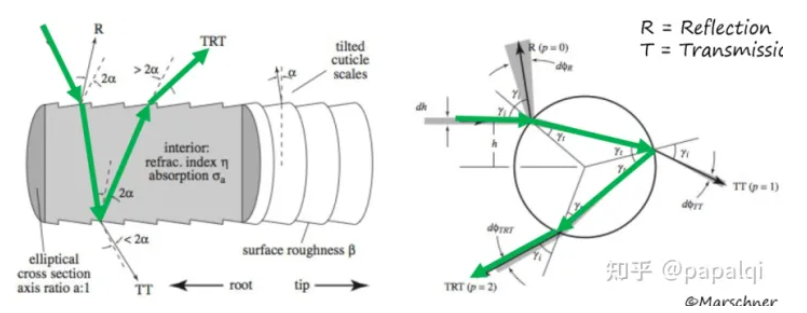
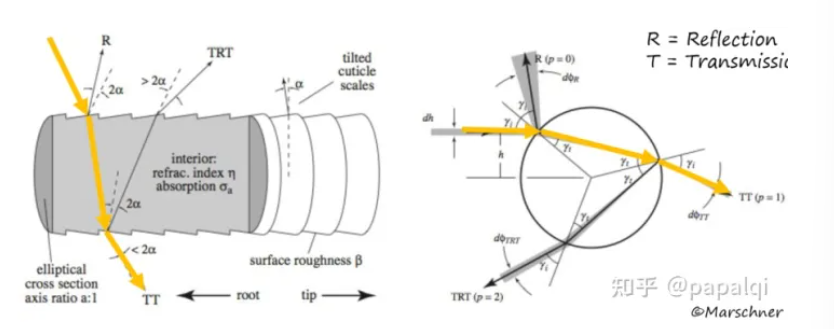
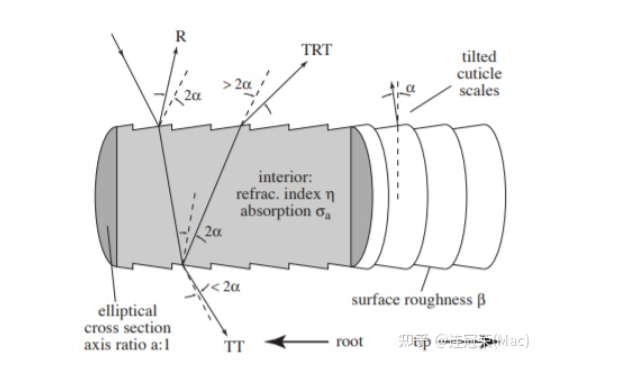
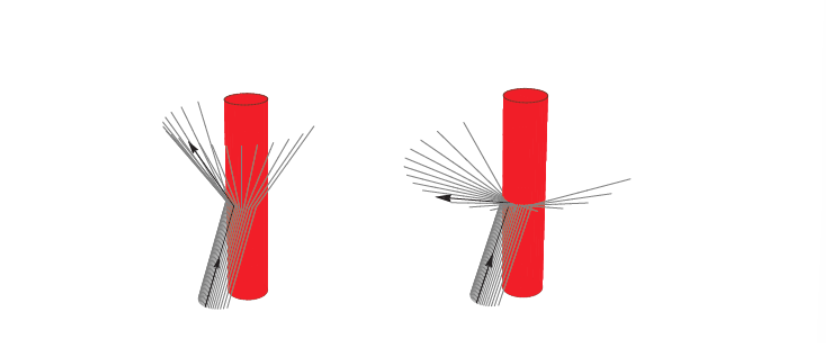
在这种情况下我们发现实际上头发对光的散射情况应该如下图所示:


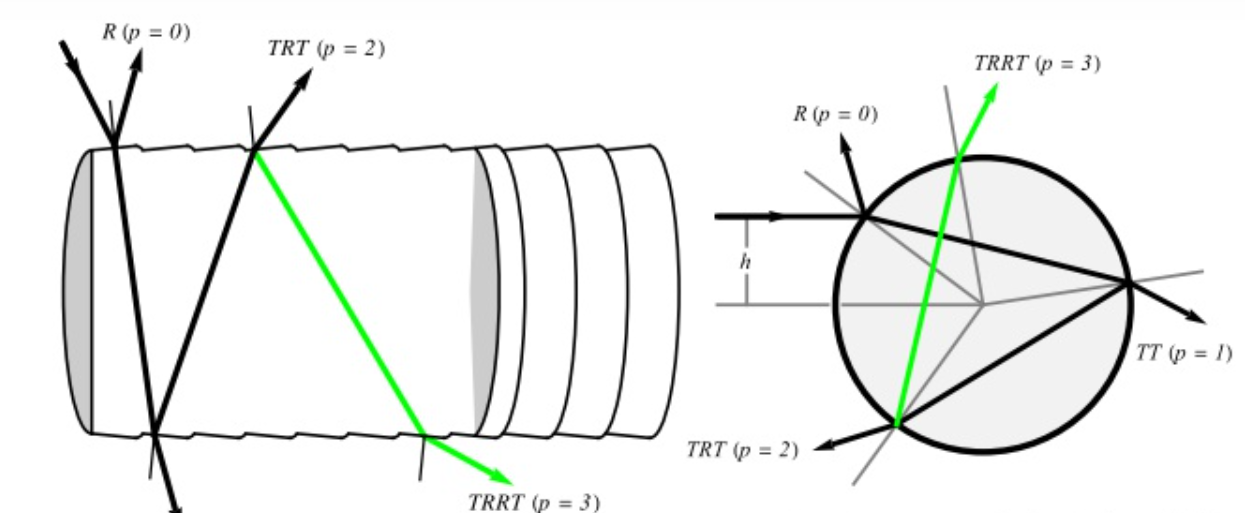
T即Transmission透射,他的一种主要表现情况就是折射,而R就是Reflection反射,因此实际上光照到头发某一点后首先会产生反射R也是高光主要产生因素,同时还会折射进入头发纤维一部分在内部发生反射再折射出头发形成TRT即一种偏移后射出的折射光,同时还会有一部分在内部直接透射出来如上图所示就是背光的效果。
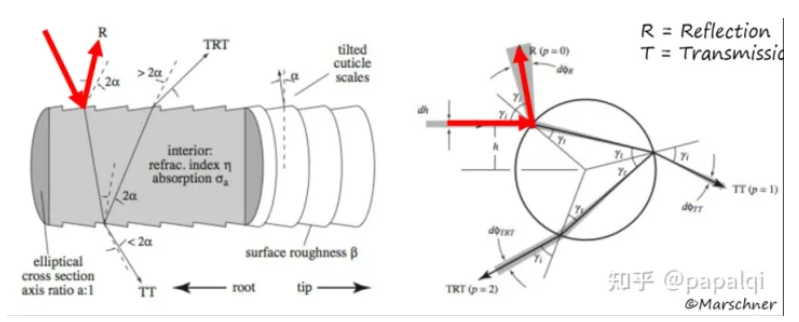
他们的主要形成原理图如下所示:

首先他是在表面直接发生了镜面反射,同时我们发现他的反射方向实际上会由于表面的凹凸不平导致反射光之间并不是平行的,而是散乱的。

其次是TRT,他的路程较为复杂,是折射-内部反射-折射的过程形成,最终会发现形成一个偏移的光,并且方向也会有扰动2α。

以及TT,他就是背光下可以看到亮光的原理,实际上是光线透过了头发丝,这个情况在深色下表现并不明显,但是在浅色头发情况时非常明显。
渲染公式推导
这就是以上各种反射散射光的形成原理,当然也会有多次内部反射再透射的情况,但是考虑到这种光线能量会很小因此可忽略。我们这里暂时记录一下几个重要的参数后面的公式推导会使用到:

⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧α:角质层倾斜角σa:吸收η:折光率β:粗糙度
实际上Masrchner类似于PBR,因此需要使用到类似于BRDF、辐射度量学、入射光线、反射光线、蒙特卡洛积分等,所以计算公式相较于前面的模型会比较复杂,他是使用了渲染公式来进行着色计算,因此首先我们回忆下最基础的渲染公式:
Lo(p,wo)=Le(p,wo)+∫Ω+fr(p,wi,wo)Li(p,wi)(n⋅wi)dwi
由于头发同时有反射、透射等所以不能使用简单的BRDF来计算,这里我们需要使用BSDF。如下图所示:
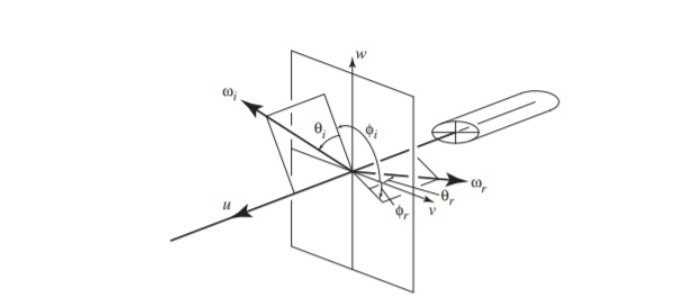
这里我们首先介绍一下重要的参数下面会用到,此时角度关系就不再是简单的夹角了而是需要同时用倾斜角和方位角进行拆分描述:
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧u:头发的切线方向(由发根到发尖)v:椭圆长轴w:椭圆短轴v−w:法平面wi(θi,φi):照射方向wr(θr,φr):散射光方向或者摄像机方向θi:wi的经度角也即倾斜角与w轴的夹角θr:wr的经度角也即倾斜角与w轴的夹角φi:wi的方位角也即与v轴的夹角φr:wr的方位角也即与v轴的夹角θd=(θr−θi)/2:倾斜角之差φd=(φi−φr)/2:方位角之差

此时我们不再是使用入射光向量和头发的切线向量进行计算,而是同时需要使用入射光方向和反射光方向并且需要使用角度关系来进行着色公式计算,这是因为由于头发不再是光滑的圆柱体,而是表面粗糙并且可以投射的材质,所以给定一个入射光线以后并不会在表面发生精确的镜面反射,而是既有反射(纵向散射:沿着头发生长方向的散射)又有透射(垂直于发丝方向的散射),而透射又会造成光线的偏移,因此实际上反射的情况会同时有下图两种情况:

其中左边就是R即反射,此时我们就需要一个函数来估计在给定的出射方向(或者叫观察方向)上有多少比例的光线射出贡献R,这个函数和入射、出射方向有关,我们可以用M(θi,θr)来表示,可以简单地认为M就是一个高斯分布的概率密度函数。同时右图另一方面又有折射和透射,我们同样可以用一个函数来估计发生方位角散射给定出射方向上的比例,这个函数除了和入射、出射方向投影在圆柱法平面的方位角有关,还和头发内部的折射率有关,我们用N(θi,θr,φd)(其中φd是方位角度差)。也就是说此时我们对于头发的着色,每个像素或者点P都有R,TRT,TT三项,并且把每项都分解成M和N,其中M项是纵切面的散射分布,N项是横切面的散射分布。
因此此时我们的BSDF会同时与Mp和Np有关可以写成方位散射函数N和纵向散射函数M的组合,即如下表示:
Sp(θi,θr,φd)=SR+STT+STRT=S(ϕi,θi;ϕr,θr)=M(θi,θr)N(η′(θd);ϕi,ϕr)/cos2θd
注意上式中的η’是基于原始折射率计算得到的一种修正折射率我们会在下篇文章中详细介绍。同样的BSDF实际上定义式仍为出射光的radiance和入射的irradiance的比值即:
S(wr,wi)=dL(wr)/dE(wi)
同时我们可以进一步拆分dE(wi)
dEi(wi)=D∗Li(wi)cosθidwi(D是头发的直径和wi有关)
所以最终我们也可以推导出该着色模型的计算公式:
Lr(wr)=∫D∗S(wi,wr)Li(wi)∗cosθidwi
实际上就是将原本的渲染公式中BRDF换为BSDF,并且多了一个常数项即头发的直径D。那么接下来我们就是来深入研究一下BSDF该如何计算,根据得到的BSDF利用渲染方式即可得到一个非常真实的头发渲染效果,具体的BSDF以及M项N项的拟合与代码实现请看下一篇。这里我们简单介绍一下M项与N项的公式由来:
M项和N项的推导
对于M纵向散射函数,如果假设头发是光滑的那么M项可以看成是狄拉克分布,但是实际上头发纤维是粗糙的,所以实时计算可以使用高斯分布,其标准差是头发丝的纤维粗糙度,期望值是头发纤维的粗糙微表面对光线的偏移量。这个高斯函数可以表述为
Mp(θi,θr)≈βn2π1e−2βp2(sinθi+sinθr−αp)2
而对于N项方位散射函数,每一个光路R、TT、TRT都有一个与之对应的N项,我们将其头发剖面图转换为标准圆简化后进行数学推导:

以TT路径为例,光线入射时折射角为γt,出折射角为γi 则全程偏角为γt+γi ,显然不同光路的全程偏角是不同的,可以用下面的公式进行计算:
ϕ(p,h)=2pγt−2γi+pπ
其中p表示折射或反射的段数,P=0对应R,P=1对应TT,P=2对应TRT,里面的偏移量h是一个与修正过的广义折射率计算有关的项:
h2=(4−(η′)2)/3
其中η′ 可以有Snell定律计算得到:
η′(γ)=η2−sin2γ/cosγ
其中γ 是投影角,接下来经过一系列复杂的推导我们可以得到散射光强度计算公式:
Lˉ(ϕ(h))=∣∣∣∣∣2ahdϕ∣∣∣∣∣−1E2
我们在引入吸收项A:
Lˉ(ϕ)=A(p,h)∣∣∣∣∣2dhdϕ∣∣∣∣∣−1Eˉ
A(p,h) 是吸收方程,具体计算为:
A(0,h)=F(η′,η′′,γi)A(p,h)=(1−F(η′,η′′,γi))2F(η′1,η21,γi)p−1T(σa′,h)p
其中 η′′ 为:
η′′(γ)=η2cosγ/η2−sin2γ
综上完整的N项计算为:
N(ϕ)Np(p,ϕ)=p∑Np(p,ϕ)=r∑A(p,h(p,r,ϕ))∣∣∣∣∣2dhdϕ(p,h(p,r,ϕ))∣∣∣∣∣−1
我们会发现相当复杂,这主要是因为吸收项和散射强度公式参数过多,因此接下来我们要引入一种基于该模型的改进版,它主要是修复了该模型基于物理却能量不守恒的缺陷,同时还简化了N项的计算,采用了一种积分的形式求解。
d’Eon Shading Model
d’Eon在2011年发表了一个篇论文:《一种性能节省的头发反射模型》中基于Marschner模型做了完善,使得头发的渲染更加能量守恒,因为从实验数据上来看虽然Marschner模型理论上基于物理,但是实际上有点小瑕疵即该模型限制了低吸收性的头发比如白色、浅金色头发的掠光角度和表面粗糙度的正确性,他虽然是基于物理的,但是却并不能量守恒,因此修正如下:
首先M项调整为更复杂的:
Mp(v,θi,θr)=2vcsch(1/v)evsin(−θj)sinθrI0[vcos(−θi)cosθr]v=β2 Io(x)为修正贝塞尔函数 csch(x)是双曲余割函数
对于上式公式它取代了高斯分布实现更加精确地计算backlit效果,同时对于N项,调整了吸收函数的计算方法:
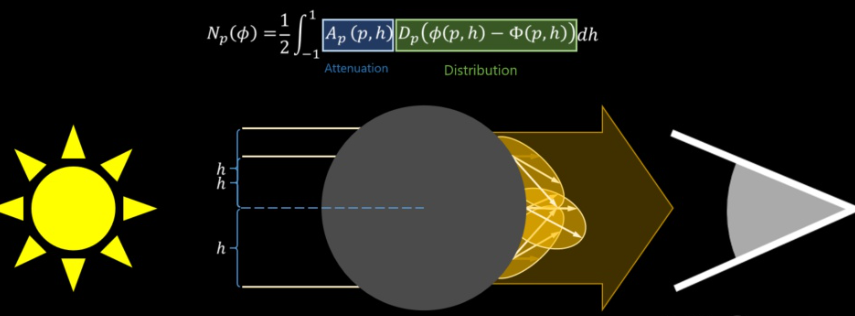
A(0,h)=F(η,21arccos(ωj⋅ωr))A(p,h)=(1−f)2fp−1T(μa′,h)pNp(ϕ)=21∫−11A(p,h)Dp(ϕ−Φ(p,h))dh
上式中分为衰减分子A和分布D两部分,A用于解释毛发中的菲涅尔反射和吸收,分布D用于模拟光在反射或离开纤维时如何散射。T(μa′,h)是用来计算头发的透射系数的函数,其中μa′表示头发的吸收系数,h表示头发的厚度(这两项是头发材质的属性,一般通过实验测得)。透射系数指的是光线穿过头发时损失的能量比例。而A(0.h)和A(p,h)分别是d’Eon Shading Model中用来计算头发反射和透射的系数,其中A(0,h)用于计算头发的反射系数,A(p,h)用于计算头发的透射系数。

同时为了得到更加逼真的效果,该模型在R,TT,TRT基础上又新增考虑了TRRT路径,同时为了简化考虑将头发看成标准园柱体这可以非常大程度得降低数学模型的复杂度

最终我们可以看看Marschner和改进后d’Eon Shading Model效果图的对比可以看到右侧的透光性更好更真实: